BE/B.Tech | Digital Electronics | For E.C.E. & E.I.E Second Year, III Semester IMP QnA.
Q.1 Draw and explain half adder and subs tractor circuit.
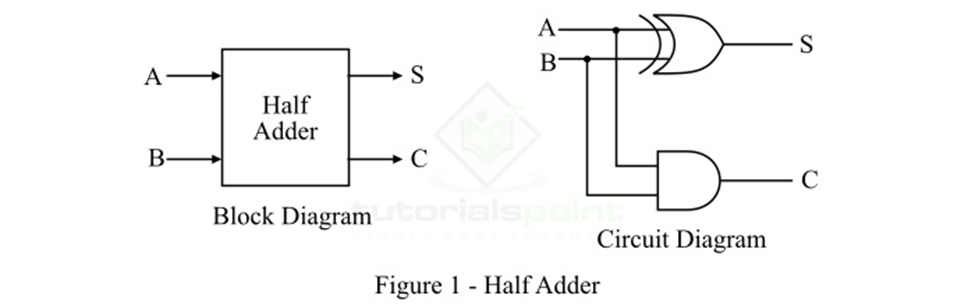
What is a Half-Adder?
A combinational logic circuit which is designed to add two
binary digits is called as a half adder. The half adder provides the output along with a carry
value (if any). The half adder circuit is designed by connecting an EX-OR gate
and one AND gate. It has two input terminals and two output terminals for sum
and carry. The block diagram and circuit diagram of a half adder are shown in
Figure-1.
In the case of a half adder, the output of the EX-OR gate
is the sum of two bits and the output of the AND gate is the carry. Although,
the carry obtained in one addition will not be forwarded in the next addition
because of this it is known as half adder.
Truth
Table of Half Adder
The following is the truth table of the half-adder −
|
Inputs |
Outputs |
||
|
A |
B |
S (Sum) |
C (Carry) |
|
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
0 |
|
1 |
1 |
0 |
1 |
Characteristic
Equations of Half-Adder
The characteristic equations of half adder, i.e., equations
of sum (S) and carry (C) are obtained according to the rules of binary
addition. These equations are given below −
The sum (S) of the half-adder is the XOR of A and B. Thus,
Sum,S=A⊕B=AB′+A′BSum,S=A⊕B=AB′+A′B
The carry (C) of the half-adder is the AND of A and B. Therefore,
Carry,C=A⋅BCarry,C=A⋅B
What is a Full Adder?
A combinational logic circuit that can add two binary
digits (bits) and a carry bit, and produces a sum bit and a carry bit as output
is known as a full-adder.
In other words, a combinational circuit which is designed
to add three binary digits and produces two outputs (sum and carry) is known as
a full adder. Thus, a full adder circuit adds three binary digits, where two
are the inputs and one is the carry forwarded from the previous addition. The
block diagram and circuit diagram of the full adder are shown in Figure-2.
Hence, the circuit of the full adder consists of one EX-OR
gate, three AND gates and one OR gate, which are connected together as shown in
the full adder circuit in Figure-2.
Truth
Table of Full Adder
The following is the truth table of the full-adder circuit
−
|
Inputs |
Outputs |
|||
|
A |
B |
Cin |
S (Sum) |
C (Carry) |
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
Hence, from the truth table, it is clear that the sum
output of the full adder is equal to 1 when only 1 input is equal to 1 or when
all the inputs are equal to 1. While the carry output has a carry of 1 if two
or three inputs are equal to 1.
Characteristic
Equations of Full Adder
The characteristic equations of the full adder, i.e.
equations of sum (S) and carry output (Cout) are obtained according
to the rules of binary addition. These equations are given below −
The sum (S) of the full-adder is the XOR of A, B, and Cin.
Therefore,
Sum,S=A⊕B⊕Cin=A′B′Cin+A′BC′in+AB′C′in+ABCinSum,S=A⊕B⊕Cin=A′B′Cin+A′BCin′+AB′Cin′+ABCin
The carry (C) of the half-adder is the AND of A and B.
Therefore,
Carry,Cout=AB+ACin+BCin
Q.2 Convert the following.
A. (1101011)2=()10
B. (623.77)8=()10
C. (225)10=()8
A. (1101011)2=()10
To convert the binary number (1101011)2
to decimal, you can use the positional notation system. Each digit in the
binary number represents a power of 2, starting from the rightmost digit as 20
and increasing by powers of 2 as you move to the left.
The binary number (1101011)2 can be
expanded as follows:
(1101011)2=1×26+1×25+0×24+1×23+0×22+1×21+1×20
Now, let's compute the value:
=1×64+1×32+0×16+1×8+0×4+1×2+1×1
=64+32+0+8+0+2+1
=107
Therefore, (1101011)2=10710
B. (623.77)8=()10
To convert the octal number (623.77)8 to
decimal, we can use the positional notation system. Each digit in the octal number
represents a power of 8, starting from the decimal point and moving to the left
for integer parts, and moving to the right for fractional parts.
Let's break down the octal number (623.77)8
into its decimal equivalent:
For the integer part:
6×82+2×81+3×80
=6×64+2×8+3×1
=384+16+3
=403
For the fractional part:
7×8−1+7×8−2
=![]() +
+![]()
=0.875+0.109375
=0.984375
Therefore, putting the integer and fractional parts together:
(623.77)8=403+0.984375
=403.98437510
So, (623.77)8=403.98437510
C. (225)10=()8
To convert the decimal number (225)10 to
octal, we need to repeatedly divide the decimal number by 8 and keep track of
the remainders.
Here's the process:
225 ÷ 8 = 28 remainder 1
28 ÷ 8 = 3 remainder 4
3 ÷ 8 = 0 remainder 3
Now, we read the remainders from bottom to top, which gives
us (225)10=(341)8(225)10=(341)8 in octal notation.
Therefore, (225)10=(341)8 in
octal.
3. Realize the function Y=![]() +A+
+A+![]() Using NAND Gates.
Using NAND Gates.
To realize Y = (AB)' + A + (B + C)' using
NAND gates only, you can follow these steps:
- Begin by creating the NAND gate equivalent of the NOT
operation, which can be achieved by connecting one input of the NAND gate
to its output.
- To create the NAND gate equivalent of the AND operation,
connect two NAND gates in series, with the output of one NAND gate
connected to the input of another NAND gate.
- To create the NAND gate equivalent of the OR operation,
connect two NAND gates in parallel, with each NAND gate receiving one of
the inputs and the outputs of both NAND gates connected together.
- Using the above operations, we can realize Y = (AB)' + A +
(B + C)' using the following circuit:
- Connect the inputs A and B to a NAND gate to get (AB)'
- Connect the output of the first NAND gate to the input of
a second NAND gate with input A to get A + (AB)'
- Connect inputs B and C to a NAND gate to get (B + C)'
Connect the output of the second NAND gate and the output of the third NAND gate to a third NAND gate to get Y = (AB)' + A + (B + C)'
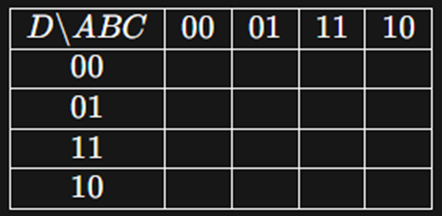
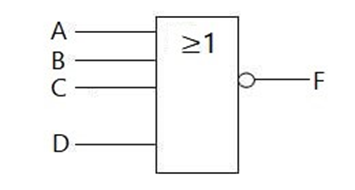
Q. Using K-Map method simplicity the following function
obtain its.
i) Minimum sum of product =
Q. Using K-Map method simplicity the following function
obtain its. i) Minimum sum of product =∑1,2,5,6,7,10,14,15
ChatGPT
ChatGPT
To simplify the given function
F=∑imi=
∑i (1,2,5,6,7,10,14,15)
using the Karnaugh Map (K-Map) method, we first need to arrange the minterms in
the K-Map and then identify groups of adjacent 1s.
The K-Map is a graphical representation of the truth table
where adjacent squares represent terms that differ by only one variable.
Since the function F has 4 variables, we represent
the K-Map with rows and columns representing all possible combinations of the 4
variables (A, B, C, D).
Now, let's mark the cells corresponding to the given
minterms:
Now, we need to group adjacent 1s in the K-Map. We can form
groups of 1s such that each group contains 1, 2, 4, or 8 cells.
After grouping the 1s, we should select the smallest number
of groups to cover all the 1s.
For the given K-Map, we have the following groups:
- Group
1: m1,m2,m5,m6
- Group
2: m10,m14,m15
- Group
3: m7
Therefore, the simplified expression for F is:
F=(A′B′CD)+(AB′CD′)+(ABC′D′)
Q. Explain TTL and CMOS Logic families in brief.
TTL (Transistor-Transistor Logic):
TTL is a popular family of digital integrated circuits used
for logic operations in electronic devices. It originated in the 1960s and
remained prevalent until the 1980s. Here are some key points about TTL:
- Transistors:
TTL circuits are built using bipolar junction transistors (BJTs) as their
primary active components. These transistors switch between saturated and
cut-off states to represent digital signals.
- Low
and High States: In TTL logic, a low logic level typically ranges from
0V to 0.8V, while a high logic level is usually between 2V to 5V. This
implies that TTL logic requires a higher voltage swing than other families
like CMOS.
- Power
Consumption: TTL circuits consume more power compared to CMOS logic
due to the constant current flow in the active devices, even when they are
in a static state.
- Noise
Immunity: TTL logic has good noise immunity, making it suitable for
industrial and automotive applications where noise levels can be
significant.
- Speed:
TTL logic operates at relatively high speeds, making it suitable for
applications where speed is a critical factor, such as in high-speed data
communication systems.
- Obsolete:
While TTL was once widely used, it has largely been replaced by CMOS
technology due to its higher power consumption and other limitations.
CMOS (Complementary Metal-Oxide-Semiconductor):
CMOS is another prevalent family of digital integrated
circuits used for logic operations. It became popular in the 1980s and is
widely used today. Here are some key points about CMOS:
- Transistors:
CMOS circuits use complementary pairs of metal-oxide-semiconductor
field-effect transistors (MOSFETs) as their primary active components.
These transistors have low static power consumption and provide excellent
noise margins.
- Low
Power Consumption: One of the key advantages of CMOS logic is its low
power consumption. CMOS circuits consume power only during state
transitions, making them ideal for battery-powered devices and portable
electronics.
- Voltage
Levels: CMOS logic operates at a wider range of voltage levels
compared to TTL, typically between 0V to Vcc (supply voltage). This
flexibility allows for compatibility with a variety of systems and power
supplies.
- Noise
Immunity: CMOS logic has excellent noise immunity due to the inherent
properties of MOSFETs, making it suitable for applications where noise is
a concern.
- Speed:
While CMOS logic historically operated at slower speeds compared to TTL,
advancements in technology have led to the development of high-speed CMOS
(HCMOS) variants, which offer comparable speeds to TTL.
- Dominant
Technology: CMOS has become the dominant logic technology due to its
low power consumption, high noise immunity, and compatibility with modern
semiconductor manufacturing processes.
Q. Discuss analog to digital & digital to analog converter?
Briefly.
Analog-to-Digital Converter (ADC):
The transducer’s electrical analog output serves as the
analog input to the ADC. The ADC converts this analog input to a digital
output. This digital output consists of a number of bits that represent the
value of the analog input. For example, the ADC might convert the transducer’s
800- to 1500-mV analog values to binary values ranging from 01010000 (80) to
10010110 (150). Note that the binary output from the ADC is proportional to the
analog input voltages so that each unit of the digital output represents 10mV.
The digital representation of the analog vales is transmitted from the ADC to
the digital computer, which stores the digital value and processes it according
to a program of instructions that it is executing
An Analog-to-Digital Converter (ADC) is a device that
converts continuous analog signals into discrete digital representations.
Here's a brief overview:
- Functionality:
ADCs sample the analog signal at regular intervals and generate digital
representations of the sampled values. The digital output typically
consists of binary numbers, where each sample represents the amplitude of
the analog signal at a specific point in time.
- Sampling:
ADCs use a process called sampling to capture the analog signal at
discrete time intervals. The rate at which samples are taken is called the
sampling frequency or sampling rate.
- Quantization:
After sampling, the analog signal is quantized into discrete levels. The
resolution of the ADC determines the number of possible discrete levels,
often expressed in bits. For example, an 8-bit ADC can represent the
analog signal with 256 different levels (2^8).
- Conversion
Process: The conversion process in an ADC typically involves three
main stages: sampling, quantization, and encoding. During sampling, the
analog signal is measured at discrete time intervals. In quantization, the
continuous amplitude of the signal is mapped to a discrete set of levels.
Finally, in encoding, the quantized values are represented in digital form
using binary codes.
- Types
of ADCs: There are various types of ADC architectures, including
successive approximation ADCs, delta-sigma ADCs, flash ADCs, and pipeline
ADCs. Each type has its own advantages and trade-offs in terms of speed,
accuracy, and cost.
Digital-to-Analog Converter (DAC):
This digital output from the computer is connected to a DAC,
which converts it to a proportional analog voltage or current. For example, the
computer might produce a digital output ranging from 0000000 to 11111111, which
the DAC converts to a voltage ranging from 0 to 10V
A Digital-to-Analog Converter (DAC) is a device that
converts digital signals into analog voltage or current levels. Here's a brief
overview:
- Functionality:
DACs take digital input values and produce corresponding analog output
signals. These output signals are continuous and represent a voltage or
current level proportional to the digital input value.
- Resolution:
Similar to ADCs, DACs have a resolution that determines the number of
discrete output levels they can produce. Higher-resolution DACs can
generate more accurate analog output signals.
- Conversion
Process: The conversion process in a DAC involves converting digital
input values into corresponding analog output voltages or currents. This
process typically involves a digital-to-analog conversion circuit, which
may use resistive networks, voltage sources, or current sources to
generate the analog output.
- Types
of DACs: There are several types of DAC architectures, including
binary-weighted DACs, R-2R ladder DACs, multiplying DACs, and sigma-delta
DACs. Each type has its own advantages and is suitable for different
applications.
- Applications:
DACs are used in various applications, including audio systems, video
processing, telecommunications, instrumentation, and control systems. They
are essential components in systems where digital signals need to be
converted back into analog form for processing or output.
Q. Explain the Synchronous, asynchronous counter and D-Flip-Flop.
- Synchronous
Counter:
- A
synchronous counter is a type of digital counter where all the flip-flops
(or stages) change states simultaneously, triggered by the same clock
signal.
- In
synchronous counters, all flip-flops receive the same clock signal,
ensuring that changes in state occur at precisely defined moments in
time.
- Synchronous
counters are easier to design
and analyze compared to asynchronous counters because their
behavior is more predictable and easier to synchronize.
- Asynchronous
Counter:
- An
asynchronous counter is a digital counter where the flip-flops (or
stages) change states independently, without being synchronized by a
common clock signal.
- Each
flip-flop in an asynchronous counter triggers the next flip-flop, usually
using the output of the previous flip-flop as its clock input.
- Asynchronous
counters are typically more complex to design and analyze compared to
synchronous counters because their behavior depends on propagation delays
and can be prone to glitches.
S.NO | Synchronous Counter | Asynchronous Counter |
1. | In synchronous counter we use a universal clock that is common to all flip flops through out the circuit. | In asynchronous counter main clock is only applied to the first flip flop and then for rest of flip flops the output of previous flip flop is taken as a clock. |
2. | Synchronous Counter is faster in operation as compared to Asynchronous Counter. | Asynchronous Counter is slower as compared to synchronous counter in operation. |
3. | Synchronous Counter does not produce any decoding errors. | Asynchronous Counter produces decoding error. |
4. | Synchronous Counter is also called Parallel Counter. | Asynchronous Counter is also called Serial Counter. |
5. | Synchronous Counter designing as well implementation are complex due to increasing the number of states. | Asynchronous Counter designing as well as implementation is very easy. |
6. | Synchronous Counter will operate in any desired count sequence. | Asynchronous Counter will operate only in fixed count sequence (UP/DOWN). |
7. | Synchronous Counter examples are: Ring counter, Johnson counter. | Asynchronous Counter examples are: Ripple UP counter, Ripple DOWN counter. |
8. | In synchronous counter, propagation delay is less. | In asynchronous counter, there is high propagation delay. |
Flip Flop is an electronic device or to be precise a kind of
memory component that can hold one bit of data. A flip flop has two states,
that is “SET” and “RESET”. Those states are represented with the binary values
0 and 1. The flip flop remains in its current state until its receives a signal
that switches it to opposite state. A clock or pulse signal may “trigger” the
flip flop to change state.
D Flip Flop
D flip flop is an electronic devices that is known as “delay
flip flop” or “data flip flop” which is used to store single bit of data.D flip
flops are synchronous or asynchronous. The clock single required for the
synchronous version of D flip flops but not for the asynchronous one.The D flip
flop has two inputs, data and clock input which controls the flip flop.
when clock input is high, the data is transferred to the output of the flip
flop and when the clock input is low, the output of the flip flop is held in
its previous state.
Working of D Flip Flop
D flip flop consist of a single input D and two outputs (Q
and Q’). The basic working of D Flip Flop is as follows:
- When
the clock signal is low, the flip flop holds its current state and ignores
the D input.
- When
the clock signal is high, the flip flop samples and stores D input.
- The
value that was previously fed into the D input is reflected at the flip
flop’s Q output.
- If
D = 0 then Q will be 0.
- If
D = 1 then Q will be 1.
- The
Q’ output of the flip flop is complemented by the Q output.
- If
Q = 0 then Q’ will be 1.
- If
Q = 1 then Q’ will be 0.
Truth Table of D Flip Flop
Characteristic Table of D Flip Flop
The characteristic table of the D flip flop displays the
behavior of the flip flop for each combination of input and current state. The
characteristic table for a D flip flop is as follows.
Characteristics table of D Flip Flop
- D
is the input, and Q is current state, Qn + 1 is the next state outputs.
- Qn+1
will always be zero when D is 0, irrespective of current state of flip
flop.
- When
the input of the flip flop is 1, next state of flip flop will
always be 1, regardless of the current state of flip flop.
Characteristic Equation of D Flip Flop
The characteristics equation of D flip flop consist of a
Boolean expression that explains the relationship between the input and output
of the flip flop. The characteristic equation for a D flip flop is as follows.
Characteristics Equation of D Flip Flop
- Qn+1
represents the output of flip flop at the next clock cycle.
- Dn
is the input to the flip flop at the current clock cycle, and n represents
the current clock cycle.
- This
characteristic equation of D flip flop states “that the output of the
flip flop at the next clock cycle will be equal to the input at the
current clock cycle“.
D Flip Flop Excitation Table
Her, Qn represents the current state of the flip flop, and
Dn represents the current input of the flip flop. Where as Qn+1 represents the
next state of the flipflop.
- When
the Qn is 0 and the Dn is also 0, then the Qn+1 becomes 0. This situation
explains the condition of “hold” state.
- When
the Qn is 0 but Dn is 1, then the Qn+1 becomes 1. This situation explains
the condition of “reset” state.
- When
the Qn is 1 but Dn is 0, then the Qn+1 becomes 0. This situation explains
the condition of “hold” state.
- When
the Qn is 1 and the Dn is also 1, then the Qn+1 becomes 1. This situation
explains the condition of “reset” state.
Advantages of D Flip Flop
- D
flip flop is very simple to design.
- The
computation speed of D flip flop is very fast compared to other flip
flops.
- D
flip flop requires very few components to design which makes it simple to
understand.
Disadvantages of D Flip Flop
- D
flip flops are glitch prone. When input varies fast, flip flop output may
glitch. Digital circuit glitches are hard to identify and fix.
Types of D Flip Flop
- D
Latch.
- EdgeTriggered
D Flip Flop.
Application of D Flip Flop
D flip flop is having numerous number of application in
digital system is described as follows:
- Memory: D
flip flop is used to create memory circuit for holding the data.
- Registers: D
flip flop is used to create register, which can hold data in digital
system. By using the D flip flop the designer can built any size of
register as per the requirement.
- Counters: D
flip flops are used to create the counters which counts the number of
event occurred in the digital system.
- Synchronous
System: D flip flop is having in developing the synchronous
system.
Q. Explain digital and analog coverts in details.
Analog to Digital Conversion
Digital Signal: A digital signal is a signal
that represents data as a sequence of discrete values; at any given time it can
only take on one of a finite number of values.
Analog Signal: An analog signal is any
continuous signal for which the time varying feature of the signal is a
representation of some other time-varying quantity i.e., analogous to another
time varying signal.
Importance of Analog to Digital Conversion
- The
main role of ADC in modern technology development process is the
transition of voice communication systems from outdated analogue signal
processing to the more advanced voice over IP, or VoIP, systems of today
is largely due to the contribution.
- The
teletypewriters and other computer input devices needed to be connected to
a modem which was connected to a mainframe or other front end computer
system to communicate with the required computer systems. In contrast to
the ultrahigh-speed networks of today, modem transmission speeds were
modest to process.
- The
systems for smaller office applications and the digital private branch
exchange, or PBX, were developed by using ADC technology as the foundation
to process properly.
Techniques of Analog-to-Digital Conversion
The following techniques can be used for Analog to Digital
Conversion –
a. PULSE CODE MODULATION
The most common technique to change an analog signal to
digital data is called pulse code modulation (PCM). A PCM encoder has the
following three processes:
- Sampling
- Quantization
- Encoding
Low pass filter : The low pass filter eliminates
the high frequency components present in the input analog signal to ensure that
the input signal to sampler is free from the unwanted frequency components.
This is done to avoid aliasing of the message signal.
- Sampling
– The first step in PCM is sampling. Sampling is a process of
measuring the amplitude of a continuous-time signal at discrete instants,
converting the continuous signal into a discrete signal. There are three
sampling methods:
(i) Ideal Sampling: In
ideal Sampling also known as Instantaneous sampling pulses from the analog
signal are sampled. This is an ideal sampling method and cannot be easily
implemented.
(ii) Natural Sampling: Natural
Sampling is a practical method of sampling in which pulse have finite width
equal to T.The result is a sequence of samples that retain the shape of the
analog signal.
(iii) Flat top sampling: In
comparison to natural sampling flat top sampling can be easily obtained. In
this sampling technique, the top of the samples remains constant by using a
circuit. This is the most common sampling method used.
Nyquist Theorem: One
important consideration is the sampling rate or frequency. According to the
Nyquist theorem, the sampling rate must be at least 2 times the highest
frequency contained in the signal. It is also known as the minimum sampling
rate and given by: Fs =2*fh
- Quantization
– The result of sampling is a series of pulses with amplitude
values between the maximum and minimum amplitudes of the signal. The set
of amplitudes can be infinite with non-integral values between two limits.
The following are the steps in Quantization:
- We assume
that the signal has amplitudes between Vmax and Vmin
- We
divide it into L zones each of height d where, d= (Vmax- Vmin)/ L
- The
value at the top of each sample in the graph shows the actual amplitude.
- The
normalized pulse amplitude modulation(PAM) value is calculated using the
formula amplitude/d.
- After
this we calculate the quantized value which the process selects from the
middle of each zone.
- The
Quantized error is given by the difference between quantized value and
normalised PAM value.
- The
Quantization code for each sample based on quantization levels at the
left of the graph.
3.
Encoding – The digitization of the analog signal is done by the encoder. After each sample is quantized and the number of bits per sample is decided, each sample can be changed to an n bit code. Encoding also minimizes the bandwidth used. Note that the number of bits for each sample is determined from the number of quantization levels. If the number of quantization levels is L, the number of bits is n bit = log 2 L.
b. DELTA MODULATION
Since PCM is a very complex technique, other techniques have been developed to reduce the complexity of PCM. The simplest is delta Modulation. Delta Modulation finds the change from the previous value. Modulator – The modulator is used at the sender site to create a stream of bits from an analog signal. The process records a small positive change called delta. If the delta is positive, the process records a 1 else the process records a 0. The modulator builds a second signal that resembles a staircase. The input signal is then compared with this gradually made staircase signal.
We have the following rules for output:
- If
the input analog signal is higher than the last value of the staircase
signal, increase delta by 1, and the bit in the digital data is 1.
- If
the input analog signal is lower than the last value of the staircase
signal, decrease delta by 1, and the bit in the digital data is 0.
Demodulator – The demodulator takes the digital
data and, using the staircase maker and the delay unit, creates the analog
signal. The created analog signal, however, needs to pass through a low-pass
filter for smoothing.
c. ADAPTIVE DELTA MODULATION
The performance of a delta modulator can be improved
significantly by making the step size of the modulator assume a time-varying
form. A larger step-size is needed where the message has a steep slope of
modulating signal and a smaller step-size is needed where the message has a
small slope. The size is adapted according to the level of the input signal.
This method is known as adaptive delta modulation (ADM).
Applications
- Digital
Signal Processing: In this process, the systems for processing,
storing, or transporting almost any analogue signal into digital format
require ADCs to perform well. Let’s an example, in TV tuner cards this is
use as fast video analog-to-digital converters.
- Recording
Music System: The modern digital audio workstation-based sound
recording and music reproduction technologies both are basically rely
heavily on analog-to-digital converters.
- Scientific
Instruments or Projects: The digital imaging systems are normally
use analog-to-digital converters for digitizing the instruments and
projects pixels.
Q. Explain multiplexer and demultiplexer.
Multiplexer and Demultiplexer
1. Multiplexer : Multiplexer is a data selector which takes several inputs and gives a single output.In multiplexer we have 2n input lines and 1 output lines where n is the number of selection lines.
2. Demultiplexer : Demultiplexer is a data distributor which takes a single input and gives several outputs.In demultiplexer we have 1 input and 2n output lines where n is the selection line.
Difference between of Multiplexer and Demultiplexer :
|
Multiplexer |
Demultiplexer |
|
Multiplexer processes the digital information from
various sources into a single source. |
Demultiplexer receives digital information from a
single source and converts it into several sources |
|
It is known as Data Selector |
It is known as Data Distributor |
|
Multiplexer is a digital switch |
Demultiplexer is a digital circuit |
|
It follows combinational logic type |
It also follows combinational logic type |
|
It has 2n input data lines |
It has single input line |
|
It has a single output data line |
It has 2n output data lines |
|
It works on many to one operational principle |
It works on one to many operational principle |
|
In time division Multiplexing, multiplexer is used at
the transmitter end |
In time division Multiplexing, demultiplexer is used at
the receiver end |
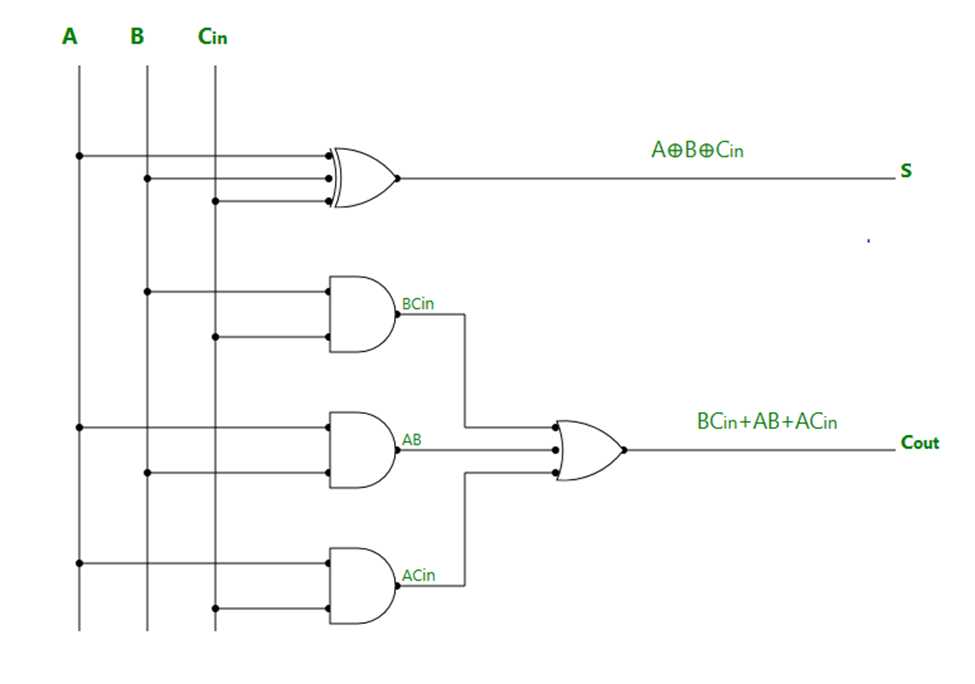
Q. Describe full adder and full substractor with diagram
and table.
- To
overcome the above limitation faced with Half adders, Full Adders are
implemented.
- It
is a arithmetic combinational logic circuit that performs addition of
three single bits.
- It
contains three inputs (A, B, Cin) and produces two outputs (Sum
and Cout).
- Where,
Cin -> Carry In and Cout -> Carry
Out
Truth table of Full Adder:
K-map Simplification for output variable Sum ‘S’ :
The equation obtained is,
S = A'B'Cin + AB'Cin' + ABC + A'BCin'
The equation can be simplified as,
S = B'(A'Cin+ACin') + B(AC + A'Cin')
S = B'(A xor Cin) + B (A xor Cin)'
S = A xor B xor Cin
K-map Simplification for output variable ‘Cout‘
The equation obtained is,
Cout = BCin + AB + ACin
Logic Diagram of Full Adder:
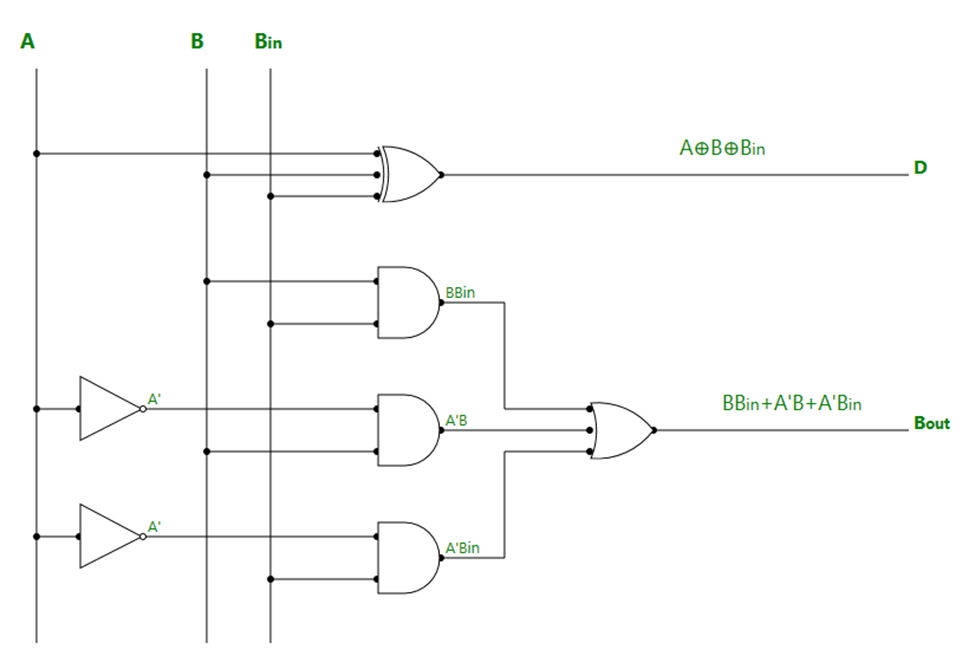
4. Full
Subtractor:
- It
is a Combinational logic circuit designed to perform subtraction of three
single bits.
- It
contains three inputs(A, B, Bin) and produces two outputs (D, Bout).
- Where,
A and B are called Minuend and Subtrahend bits.
- And,
Bin -> Borrow-In and Bout ->
Borrow-Out
Truth Table of Full Subtractor:
K-map Simplification for output variable ‘D’ :
The equation obtained from above K-map is,
D = A'B'Bin + AB'Bin' + ABBin
+ A'BBin'
which can be simplified as,
D = B'(A'Bin + ABin') + B(ABin
+ A'Bin')
D = B'(A xor Bin) + B(A xor Bin)'
D = A xor B xor Bin
K-map Simplification for output variable ‘Bout‘ :
The equation obtained is,
Bout = BBin + A'B + A'Bin
Logic Diagram of Full Subtractor:
Q. What is multivibrator? Explain monostable and bistable
multivibrator
What is a Multivibrator?
A multivibrator is a switching circuit that is a two-stage
resistance-coupled amplifier with positive feedback from the output of one
amplifier to the input of the other. The name multivibrator is derived from the
fact that the square wave generated consists of a large number of sinusoidal of
different frequencies. Multivibrators are crucial parts of digital circuits and
computer architecture, to sum up. They are utilized for data storage,
synchronization between various components, clock signal generation, timing
control, and data transfer time. The three basic types of multivibrators are
astable, monostable, and bistable, each with distinct properties and uses.
- A
multivibrator circuit oscillates between a “HIGH” state and a “LOW” state
producing a continuous output.
- In
a multivibrator, the two transistors are connected in feedback so that one
transistor controls the state of the other.
- Multivibrators
are used are widely used to implement two-state devices like Relaxation
Oscillators, Timers, and flip-flops.
The multivibrators are classified into three categories-
- Astable
Multivibrator.
- Monostable
Multivibrator.
- Bistable
Multivibrator.
Astable Multivibrator
An astable multivibrator, also called a free-running
multivibrator, is a circuit that continuously produces square waves or pulses
without the use of an external trigger. The term “astable” refers to the
absence of a stable state in this particular type of multivibrator.
- The
circuit is built to alternate between two stable states, resulting in a
steady oscillation.
- By
changing the values of the resistors and capacitors in the circuit, the
frequency and duty cycle of the output waveform can be altered.
- In
digital circuits, the astable multivibrator is frequently employed as a
clock source. The timing of data transfers between various components can
be synchronized using the frequency of the output waveform.
The output of an astable multivibrator does not have any
stable state and it changes its state from high to low and low to high
repeatedly.
Features
- It
is also known as a free-running multivibrator.
- It
has no stable state, hence the name astable.
- It
produces a continuous series of pulses with a predetermined frequency and
duty cycle.
- It
requires two identical transistors two capacitors, and a few resistors.
- It
is commonly used in oscillator circuits, pulse generators, and clock
circuits.
Applications
- Used
in square wave frequency generator.
- Used
as a timing oscillator in the computer system.
- Used
in flashing lights.
Monostable Multivibrator
A monostable multivibrator, also called a one-shot
multivibrator, is a circuit that responds to an external trigger by producing a
single pulse with a set duration. A pulse from outside causes this sort of
multivibrator to flip from its stable state to an unstable one.
- The
circuit returns to its stable condition after a certain amount of time and
generates a single output pulse.
- By
altering the values of the resistors and capacitors in the circuit, the
output pulse’s duration can be changed.
- In
digital circuits, the monostable multivibrator is frequently used for
pulse shaping, debouncing, and time delay functions.
- Other
circuits can use it as a trigger as well.
The output of a monostable multivibrator has only one stable
state.
Features
- Also
known as a one-shot multivibrator.
- It
has only one stable state.
- It
produces a single output pulse of a predetermined width when triggered by
an input signal.
- It
requires two transistors, two capacitors, and a few resistors.
- It
is commonly used in timing circuits, delay circuits, and pulse width
modulation circuits.
Applications
- Used
for regenerating weak signals.
- Used
in the pulse generator.
- Used
in memory.
Bistable Multivibrator
A flip-flop, or bistable multivibrator, is a circuit with
two stable states that can alternately exist indefinitely.
- A
signal from outside causes it to change from one stable condition to
another.
- The
circuit will stay in its stable state until another trigger signal enters
it.
- A
bistable multivibrator typically produces a square wave with two separate
voltage levels as its output waveform.
Digital circuits frequently use bistable multivibrators for
memory storage, data transport, and synchronization. They can also be utilized
in shift registers and counters.
The output of a bistable multivibrator has two stable
states. We have to apply external inputs in order to change the existing state
of the output.
Features
- Also
known as a flip-flop multivibrator.
- It
has two stable states and can remain in either state indefinitely without
any input signal.
- It
requires two transistors, two capacitors, and a few resistors.
- It
is commonly used in digital circuits as a memory element, latch, or
flip-flop.
- It
is also used in applications where a simple on/off switch is required.
Applications
- Used
for changing the supply to two circuits.
- Used
in digital operation in computers.
Q. Explain VHDL and ALU
- VHDL
(VHSIC Hardware Description Language):
VHDL is a hardware description language used in digital
circuit design and electronic system design. It stands for VHSIC (Very
High-Speed Integrated Circuit) Hardware Description Language. VHDL allows
engineers to describe the behavior and structure of digital systems, such as
integrated circuits and electronic systems, in a textual format.
Features of VHDL:
- VHDL
is a powerful language that supports both behavioral and structural
descriptions of digital systems.
- It
provides constructs for describing components, signals, processes, and
concurrent and sequential behavior.
- VHDL
supports hierarchical design, allowing engineers to build complex systems
by composing smaller, reusable components.
- It
is used extensively in the design, simulation, and synthesis of digital
circuits and systems, including ASICs (Application-Specific Integrated
Circuits) and FPGAs (Field-Programmable Gate Arrays).
VHDL is widely used in digital design and verification
processes, enabling engineers to model and simulate digital systems before
implementing them in hardware.
- ALU
(Arithmetic Logic Unit):
An Arithmetic Logic Unit (ALU) is a digital circuit that
performs arithmetic and logical operations on binary numbers. It is a
fundamental building block of the central processing unit (CPU) in computers
and microprocessors.
Functions of an ALU:
- Arithmetic
Operations: An ALU can perform basic arithmetic operations such as
addition, subtraction, multiplication, and division on binary numbers.
- Logical
Operations: It can also perform logical operations such as AND, OR,
NOT, XOR, and shift operations (left shift, right shift) on binary data.
- Comparison:
ALUs can compare two binary numbers to determine their relative
magnitudes (greater than, less than, or equal to).
Architecture of an ALU:
- An
ALU typically consists of a set of registers, multiplexers, adders, logic
gates, and control circuitry.
- It
operates on binary data stored in registers and produces results based on
the control signals received from the CPU.
- The
design and functionality of an ALU can vary depending on the specific
requirements of the CPU architecture and the intended application.
ALUs are critical components in digital computing systems,
performing the core arithmetic and logical operations necessary for executing
instructions and processing data in computers and microprocessors.
Q. Write MSI Device and Down BCD Adder.
- MSI
Device (Medium Scale Integration):
MSI devices are integrated circuits that contain a moderate
number of logic gates, typically between tens and hundreds, on a single chip.
These devices are used to implement various combinational or sequential logic
functions without the need for extensive external components.
Examples of MSI devices include multiplexers, decoders,
encoders, and adders. They are often used as building blocks in digital system
design to reduce component count, save board space, and simplify circuit
complexity.
Here are a few key points about MSI devices:
- They
offer a balance between complexity and functionality, providing a higher
level of integration than SSI (Small Scale Integration) devices but less
than LSI (Large Scale Integration) or VLSI (Very Large Scale Integration)
devices.
- MSI
devices can be cascaded or combined to create more complex logic
functions or circuits, enabling the design of larger and more
sophisticated digital systems.
- Examples
of MSI devices include 4-bit adders, multiplexers with multiple inputs
and outputs, and binary-to-BCD converters.
- Down
BCD Adder:
A Down BCD Adder is a digital circuit that performs addition
specifically on Binary-Coded Decimal numbers in descending order, which means
it processes BCD digits from most significant digit to least significant digit.
Here's how it typically works:
- It
consists of a series of full adders, each capable of adding three input
bits (A, B, and a carry-in) to produce a sum (S) and a carry-out.
- In
a Down BCD Adder, BCD digits are added starting from the most significant
digit (MSD) and proceeding to the least significant digit (LSD).
- If
the sum of two BCD digits exceeds 9 (1001 in binary), which is the
maximum value of a BCD digit, a carry-out is generated and propagated to
the next more significant digit.
- The
carry-out from the most significant digit is usually ignored or used for
overflow detection if needed.
Down BCD Adders are commonly used in digital systems where
addition operations involve BCD numbers, such as in calculators, digital
clocks, and financial applications where precise decimal arithmetic is
required.
I What is a Logic Gate?
Electronic circuits that implement basic and common logic
operations are called logic gate circuits. The gate implementing AND operation
is AND gate, that implementing OR operation is OR gate, and that implementing
NOT operation is NOT gate, also called inverter gate, etc.. (Logic 1 represents
high level; logic 0 represents low level)
1. AND Gate
Logical expression: F=A∙B
Only when the input terminals A and B are both 1, the output
terminal Y is 1, otherwise, Y is 0. Common chip models of AND gates are:
74LS08, 74LS09, etc.
|
A |
0 |
0 |
1 |
1 |
|
B |
0 |
1 |
0 |
1 |
|
F |
0 |
0 |
0 |
1 |
AND Truth Table
2. OR Gate
Logical expression: F=A+B
When one of the input terminals A and B is 1, the output
terminal Y is 1; when the input terminals A and B are both 0, Y will be 0.
Common chip models of OR gates are: 74LS32, etc.
|
A |
0 |
0 |
1 |
1 |
|
B |
0 |
1 |
0 |
1 |
|
F |
0 |
1 |
1 |
1 |
OR Truth Table
3. NOT Gate
Logical expression: F=A'
The output terminal is always opposite to the input
terminal. Common chip models of NOT gates are: 74LS04, 74LS05, 74LS06, 74LS14,
etc.
|
A |
0 |
1 |
|
F |
1 |
0 |
NOT Truth Table
4. NAND Gate
Logical expression: F=A'B'
That is, only when all input terminals A and B are 1, the
output terminal Y is 0, otherwise, Y is 1. Common chip models of NAND gates
are: 74LS00, 74LS03, 74S31, 74LS132, etc.
The NAND symbol:
|
A |
0 |
0 |
1 |
1 |
|
B |
0 |
1 |
0 |
1 |
|
F |
1 |
1 |
1 |
0 |
NAND Truth Table
5. NOR Gate
Logical expression: F=A'+B'
As long as one of the input terminals A and B is 1, the
output terminal Y is 0. When the input terminals A and B are both 0, Y will be
1. Common chip models of NOR gates are: 74LS02, etc.
|
A |
0 |
0 |
1 |
1 |
|
B |
0 |
1 |
0 |
1 |
|
F |
1 |
0 |
0 |
0 |
NOR Truth Table
6. XNOR Gate
Logical expression: F=A∙B+A'B'
|
A |
0 |
0 |
1 |
|
B |
0 |
1 |
1 |
|
F |
1 |
0 |
1 |
XNOR Truth Table
7. XOR Gate
Logical expression: F=A∙'B+A∙B'
XOR symbol:
|
A |
0 |
0 |
1 |
1 |
|
B |
0 |
1 |
0 |
1 |
|
F |
0 |
1 |
1 |
0 |
XOR Truth Table
8. AND-OR-NOT Gate
Logical expression: F=A'B'+C'D'
|
A |
0 |
0 |
... |
1 |
|
B |
0 |
0 |
... |
1 |
|
C |
0 |
0 |
... |
1 |
|
D |
0 |
1 |
... |
1 |
|
F |
1 |
1 |
|
0 |
AND-OR-NOT Truth Table
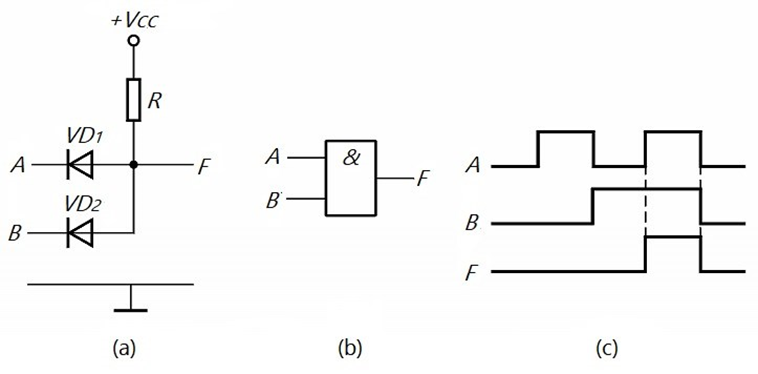
II RS Flip-flop
1. Circuit Structure
Connect the input and output ends of the two NAND gates G1
and G2 to form a basic RS flip-flop. The logic circuit is shown in the
Figure below. It has two input terminals R and S and two output terminals
Q and Q'
Figure 1.Basic RS flip-flop Simple Circuits Diagrams Consist
of 2 NAND Gates
The logic equation of the basic RS flip-flop is:
According to the two formulas, the relationship between its
four inputs and outputs is:
(1) When R=1, S=0, then Q=0, Q'=1, and the
flip-flop is set to 1.
(2) When R=0, S=1, then Q=1, Q'=0, and the
flip-flop is set to 0.
When two input terminals of the flip-flop are added with
different logic levels, its two output terminals Q and Q' have two
complementary stable states. Generally, and the state of the terminal Q is
defined as the state of the flip-flop.
When Q=1 and Q'=0, the flip-flop is set to in
1, otherwise, the flip-flop is set to 0.
When S=0, R=1, the flip-flop is set to 1. Since the decision
condition for the setting is S=0, the S terminal is called the set 1 terminal.
When R=0, S=1, the flip-flop is set to 0, called reset.
In the same way, the R terminal is called the set 0 terminal
or the reset terminal. If the flip-flop is in the 1 state, and you
want to change it to the 0 state, you must change the level of the R terminal
from 1 to 0, and the level of the S terminal from 0 to 1.
The input signal (low level) added here is called the
trigger signal, and the conversion process caused by them is called flip.
Because the trigger signal here is level, this kind of trigger is called the
level control trigger.
From a functional point of view, it can only be set to 0 and
1 under the action of S and R, so it is also called a set to 0 or reset
flip-flop. The logic symbol is shown in Figure 1(b). Since setting 0 or 1 is
valid only when the trigger signal is low level, therefore, the S end and R end
are drawn with small circles
(3) When terminal R and S are all invalid, the trigger
state remains unchanged.
When the flip-flop state remains unchanged, the input
terminals are all added with an invalid level (high level). When a flip is
required, a negative pulse must be added to one input terminal. For example,
when you add a negative pulse to the S terminal to set the trigger to 1, after
it returns to the high level, the flip-flop remains in the 1 state. This is
equivalent to storing the level signal at a certain moment in the S terminal,
which reflects the memory function of the flip-flop.
(4) When the R and S end are all valid, the trigger state
is uncertain.
Under this condition, the output terminals Q and Q' of
the two NAND gates are both 1. After both input signals are removed at the same
time (back to 1), because the delay time of the two NAND gates cannot be
determined, it's not sure whether the flip-flop state is 1 or 0. This situation
is called an indeterminate state, which should be avoided.
In other words, because the terminal R and S can be set to 0
and 1 at a low level, the two cannot be 0 at the same time.
Figure 2..Basic RS flip-flop Consists of 2 NOR Gates
2. Characteristic Equation
3. Features
(1) The basic RS flip-flop has the functions of
setting, resetting, and maintain (memory);
(2) The trigger signal of the basic RS trigger
is valid at a low level, which belongs to the level trigger mode;
(3) The basic RS flip-flop has constraints
(R+S=1), because the delay time of the two NAND gates cannot be determined,
when R=S=0, the next state will be uncertain.
(4) It has a poor anti-interference performance. When
the input signal changes, the output will change immediately.
III TTL Logic Gate Circuit
A circuit with a bipolar semiconductor as
the basic element, integrated on a silicon chip, with certain logic functions
is called a bipolar logic integrated
circuit, or TTL logic gate circuit. It is a kind of logic gate circuit
commonly used in digital electronics, which has been applied
earlier and is relatively mature.
TTL is mainly composed of a BJT (bipolar
junction transistora>) and a resistor. It has a
fast speed. The earliest TTL gate circuit was the 74 series, and then the 74H
series, 74L series, 74LS, 74AS, 74ALS and other series appeared. However,
because TTL has large power consumption, it is gradually replaced by CMOS
circuits.
IV CMOS Logic Gate Circuit
1. TTL VS. CMOS
CMOS logic gate circuit is the second widely used digital
integrated device developed after the advent of the TTL circuit. With the
improvement of the manufacturing process, the performance of the CMOS circuit
may surpass TTL and CMOS may become the dominant logic device.
The working speed of the CMOS circuit can be compared with
TTL, and its performance in power consumption and anti-interference are much
better than TTL.
In addition, almost all ultra-large-scale storage devices
and PLD devices are manufactured using CMOS technology, and the cost is
relatively low.
The CMOS gate circuit produced in the early stage was the
4000 series, which was subsequently developed into the 4000B series. CMO
devices currently compatible with TTL, such as 74HCT series, can be exchanged
with TTL devices.
Let's discuss the CMOS inverter first, and then introduce
other CMO logic gate circuits.
2. CMOS Inverter
There are two types of MOSFETs: P-channel and N-channel,
and there are depletion and enhancement type in each. The circuit composed of
N-channel and P-channel MOSFETs is called a complementary MOS or CMOS circuit.
The following figure shows the CMOS inverter circuit, which
consists of two enhancement-mode MOSFETs. One MOSFET has an N-channel structure
and the other has a P-channel structure. In order for the circuit to work
normally, the power supply voltage VDD is required to be greater than the sum
of the absolute values of the two transistors' turn-on voltages:
VDD>(VTN+|VTP|).
Figure 1. CMOS Inverter Circuit
(1) Working Principles of Logic
First, consider two limit cases:
when Vl is at 0, the corresponding voltage is approximately
0V;
when Vl is at 1, the corresponding voltage is approximately
VDD.
In the two cases, we can assume that the N-channel
transistor TN is the working transistor and the P-channel transistor TP is the
load transistor. However, since the circuit is complementary and symmetrical,
this assumption can be arbitrary, and the opposite situation will lead to the
same result.
The following figure analyzes the working condition when
Vl=VDD. Add a load line on the output characteristic iD-VDS (VGSN=VDD) of TN
(note that VDSN=VO), which is the output characteristic iD-VSD of the load
transistor TP when VSGP=0V.
Since VSGP<VT (VTN=|VTP|=VT), the load curve is almost a
horizontal line overlapping the horizontal axis. The intersection of the two
curves is the operating point.
Obviously, the output voltage at this time VOL≈0V.
Generally, this value is less than 10mV, and the current through the two
transistors is close to zero. So we can say the power consumption of the
circuit is very small (in the order of microwatts)
Figure 2. vI=VDD
The following figure analyzes another limit case, where
VI=0V.
At this time, the transistor TN is used when VGSN=0 and its
output characteristic iD-VDS almost overlaps the horizontal axis. The load
curve is the output characteristic iD-VDS of the load transistor TP when
vSGP=VDD. In the figure, the operating point determines VO=VOH≈VDD, and the
current through the two devices is close to zero.
The power consumption in the above two limit cases is very
low, so the basic CMOS inverter is almost an ideal logic unit. Its output
voltage is close to zero or +VDD, and the power consumption is almost zero.
Figure 3. vI=0V
(2) Transmission Characteristics
The following figure shows the transmission characteristics
of a CMOS inverter. In the figure, VDD=10V, VTN=|VTP|=VT=2V. Since
VDD>(VTN+|VTP|), when VDD-|VTP|>VI>VTN, both TN, and TP are turned on
at the same time. Considering that the circuit is complementary and
symmetrical, one device can be the drain load of the other device.
It should also be noted that the device exhibits constant
current characteristics in the amplification region (saturation region), and
one device can be used as a high-resistance load. Therefore, in the transition
area, the transmission characteristics change sharply. The two transistors
switch states when VI=VDD/2.
Figure 4. Transmission Characteristics of a CMOS Inverter
(3) Working Speed
When the CMOS inverter under a capacitive load, its turn-on
time and turn-off time are equal, because the circuit is complementary and symmetrical.
The following figure shows when VI=0V, TN is off, TP is on,
and the load capacitor CL
is charged by VDD through TP. In the CMOS inverter, the gm values of the two
transistors are designed to be large, so the on-resistance is small, and the
time constant of the charging loop is small. Similarly, we can analyze the
discharge process of capacitor CL. The average transmission delay time of CMOS
inverters is about 10ns.
Figure 5. Working Speed when vI=0V
3. CMOS Logic Gate Circuit
(1) NAND Gate Circuit
The figure below is a 2-input CMOS NAND gate circuit, which
includes two series N-channel enhancement MOSFETs and two parallel P-channel
enhancement MOSFETs. Each input terminal is connected to the gate of an
N-channel and a P-channel MOSFET.
Figure 5. 2-input CMOS NAND Gate Logic Diagram
When one of the input terminals A and B are low, the NMOS
transistor connected to it will be cut off, the PMOS transistor connected to it
will be turned on, and output a high level. When both A and B are high level,
the two series-connected NMOS transistors are turned on, and the two
parallel-connected PMOS transistors are turned off, outputting a low level.
Therefore, this circuit has the logic function of NAND:
The NAND gate of n input terminals must have n series NMOS
transistors and n parallel PMOS transistors.
(2) NOR Gate Circuit
The figure below is a 2-input CMOS NOR gate circuit. It
includes two parallel N-channel enhancement MOSFETs and two series P-channel
enhancement MOSFETs.
Figure 6. 2-input CMOS NOR Gate Circuit
When only one of the input terminal A and B is high, the
NMOS transistor connected to it will be turned on, with a low-level output, and
the PMOS transistor connected to it will be turned off. When both A and B are
low level, the two parallel NMOS transistors are turned off, and the two series
PMOS transistors are turned on, and output a high level.
Therefore, this circuit has the logical function of NOR, and its logical expression is:
Similarly, NOR gates with n input terminals must have n
parallel NMOS transistors and n parallel PMOS transistors.
Comparing CMOS NAND gates and NOR gates, we can see that the
working transistors of the NAND gate are connected in series with each other,
and their output voltage increases with the increase of the number of
transistors. On the contrary, the working transistors of the NOR gate are
connected in parallel, and the output voltage is not seriously affected.
Therefore NOR gates are used more often.
(3) XOR Gate Circuit
Figure 7. CMOS XOR Gate Circuit
The picture above shows the CMOS XOR circuit. It consists of a first-level NOR gate and a first-level NAND gate. The NOR gate output. And the output L of the NOR gate is the XOR of the input A and B:
Adding an inverter after the XOR gates constitutes an XNOR
gate. The logic symbols of the XOR and XNOR gate are shown in the figure below.
Figure 8. Logic gate Symbols of XOR and XNOR Gate
4. BiCMOS Gate Circuit
Bipolar CMOS or BiCMOS has the advantage of the fast speed
of bipolar devices and the low power consumption of MOSFET. Therefore, it is
valued by users.
(1) BiCMOS Inverter
Figure 9.Basic BiCMOS Inverter Circuit
The above figure shows the basic BiCMOS inverter circuit.
For clarity, the MOSFET is represented by M, and BJT is represented by T.
T1 and T2 constitute a push-pull output stage. The input
stage composed of Mp, MN, M1, and M2, similar to the basic CMOS inverter. The
input signal VI acts on the gates of MP and MN at the same time. When VI is a
high voltage, MN is turned on and MP is turned off; when VI is a low voltage,
MP is turned on and MN is turned off.
When the output terminal is connected with a BiCMOS gate
circuit, the output stage can provide enough current to charge the capacitive
load. In the same way, the charged capacitive load can quickly discharge
through T2.
The charge stored in the base area of T1 and T2 can also be
released through M1 and M2, to speed up the switching speed of the circuit.
When VI is a high voltage, M1 is turned on, and the charge in the base area of
T1 is quickly dissipated. This is similar to T1 in the input stage of the TTL
gate. When VI is a low voltage, VDD turns on M2 through MP, and the charge in
the base area of T2 is dissipated through M2.
Therefore, the switching speed of the gate circuit can be
improved.
(2) BiCMOS Gate Circuits
According to the structure and working principle of the CMOS
gate circuit mentioned above, NOR gates and NAND gates can also be realized
with BiCMOS technology.
To realize the NOR logic relationship, we should use the
input signal to drive parallel N-channel MOSFETs, while P-channel MOSFETs are
connected in series with each other, as the 2-input NOR gate circuit shown
below.
Figure 10. 2-input NOR Gate Circuit
When both A and B are low levels, MOSFETs MPA and MPB are
both turned on. T1 is turned on and MNA and MNB are both turned off, and the
output L is high. At the same time, M1 is stimulated by VDD through MPA and
MPB, thereby providing a release path for the charge in the base area of T2.
On the other hand, when one of the two input terminals A and
B is high, the path of MPA and MPB is disconnected, and MNA or MNB is turned
on, with a low-level output. Meanwhile, M1A or M1B provides a release path for
the charge of the T1 base. Therefore, as long as there is an input terminal
connected to a high level, the output is low.
5. CMOS Transmission Gate
The output characteristics of MOSFETs are linearly
symmetrical near the origin, so they are often used as analog switches. Analog
switches are widely used in sample-and-hold circuits, chopper circuits,
analog-to-digital, and digital-to-analog conversion circuits.
Figure 11. CMOS Transmission Gate
The transmission gate (TG) is an analog switch that
transmits analog signals. It consists of a P-channel and an N-channel
enhancement MOSFET in parallel, as shown in the figure above.
TP and TN are symmetrical, and their drain and source are
interchangeable. Suppose their turn-on voltage |VT|=2V and the input analog
signal can change from -5V to +5V. In order to prevent the PN junction between
the substrate and the drain-source being positively biased, the TP substrate is
connected to a voltage of +5V, and the TN substrate is connected to a voltage
of -5V. The gates of the two transistors C and are controlled by the
complementary signal voltages.
The working condition of the transmission gate is:
When the C terminal is connected to -5V, the gate voltage of
TN is -5V, and when VI is any value between -5V and +5V, TN is not conductive.
Meanwhile, if the gate voltage of TP is +5V, and TP is also not conductive. So
when the C terminal is connected to a low voltage, the switch is open.
In order to turn on the switch, the C
terminal C' can be connected to +5V. So the gate voltage of TN is
+5V, VI is between -5V and +3V, and TN is turned on. At the same time, the
voltage of TP is -5V, and TP will be turned on between -3V and +5V.
It can be seen that when VI<-3V, only TN is turned on,
and when VI>+3V, only TP is turned on. When VI is in the range of -3V to
+3V, both TN and TP are turned on.
The deeper the conduction of one transistor, the less
conduction of the other transistor. In other words, when the on-resistance of
one transistor decreases, the on-resistance of the other transistor increases.
Since the two transistors are connected in parallel, the on-resistance of the
switch is approximately a constant. This is the advantage of CMOS transmission.
In normal operation, the on-resistance value of the
analog switch is about hundreds of ohms. This value can be ignored when the
analog switch connected in series with an operational amplifier whose
input impedance is in megohm.






























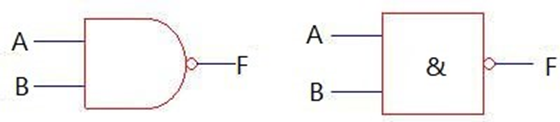






























.webp)


0 Comments