BE/B.Tech | Signal and System | For E.C.E. & E.I.E Second Year, III Semester IMP QnA.
Q1. Explain the system and its classification.
Definition of a System:
A system can be defined as a functional block that takes one
or more input signals and produces one or more output signals. The input
signals represent the information or stimuli provided to the system, while the
output signals represent the response or transformation of the input signals by
the system.
Classification of Systems:
Systems can be classified based on various criteria,
including their properties, behavior, and mathematical representations. Here
are some common classifications of systems:
- Based
on Input and Output Nature:
- Continuous-Time
Systems: These systems process signals that are defined for all real
numbers. They operate on continuous-time signals.
- Discrete-Time
Systems: These systems process signals that are defined only at
discrete points in time. They operate on discrete-time signals.
- Based
on Linearity and Time-Invariance:
- Linear
Systems: Systems that satisfy the properties of superposition and
homogeneity are considered linear.
- Time-Invariant
Systems: Systems whose properties and behavior do not change over
time are considered time-invariant.
- Based
on Memory:
- Memoryless
Systems: Systems whose output at any given time depends only on the
input at that same time are considered memoryless.
- Memory
Systems: Systems whose output depends on the current and past values
of the input are considered memory systems.
- Based
on Causality:
- Causal
Systems: Systems whose output depends only on the current and past
values of the input (i.e., they cannot anticipate future inputs).
- Non-causal
Systems: Systems whose output depends on future as well as past and
current values of the input.
- Based
on Stability:
- Stable
Systems: Systems in which bounded inputs result in bounded outputs.
- Unstable Systems: Systems in which bounded inputs may result in unbounded outputs.
Q2. Explain even and odd signal
Even Signal:
- An
even signal is symmetric about the vertical axis or the y-axis.
- Mathematically,
a signal x(t) is even if it satisfies the property: x(t)=x(−t)
for all t in its domain.
- In
the discrete-time domain, a signal x[n] is even if it
satisfies the property: = x[n]= x[−n]
for all n.
- An
even signal's plot appears identical when reflected across the y-axis.
- Example:
The cosine function is an example of an even signal.
Odd Signal:
- An
odd signal is symmetric about the origin (0,0) or the point of
intersection of the signal with the y-axis.
- Mathematically,
a signal x(t) is odd if it satisfies the property: = −x(−t)
for all t in its domain.
- In
the discrete-time domain, a signal x[n] is odd if it
satisfies the property: x[n]=−x[−n] for
all n.
- An
odd signal's plot appears as its mirror image when reflected across the
origin.
- Example:
The sine function is an example of an odd signal.
Key Points:
- An
even signal contains only cosine terms in its Fourier series
representation.
- An
odd signal contains only sine terms in its Fourier series representation.
- Some signals can be neither even nor odd, while some signals can be both.
Q3. What is an LTI system? How discrete time LTI system
Differs from continuous time LTI system?
LTI System:
An LTI system is characterized by two main properties:
- Linearity:
- A
system is linear if it follows the principles of superposition and
homogeneity.
- Superposition:
The response to a sum of inputs equals the sum of responses to each
individual input.
- Homogeneity:
Scaling the input scales the output proportionally.
- Time-Invariance:
- A
system is time-invariant if its response does not change over time.
- This
means that a time shift in the input signal results in the same time
shift in the output signal.
Discrete-Time LTI System vs. Continuous-Time LTI System:
1. Discrete-Time LTI System:
- Discrete-time
LTI systems operate on signals that are defined at discrete points in
time.
- The
input and output signals of these systems are sequences, usually
represented by x[n] and y[n]
respectively.
- The
system's behavior is defined by linear constant-coefficient difference
equations.
- The
impulse response of a discrete-time LTI system is a sequence, denoted by h[n].
- Convolution
in discrete time involves summing products of the input signal and the
system's impulse response at different time shifts.
2. Continuous-Time LTI System:
- Continuous-time
LTI systems operate on signals that are defined for all real numbers.
- The
input and output signals are continuous-time functions, usually
represented by x(t) and y(t)
respectively.
- The
system's behavior is described by linear constant-coefficient differential
equations.
- The
impulse response of a continuous-time LTI system is a function, denoted by
h(t).
- Convolution
in continuous time involves integrating the product of the input signal
and the system's impulse response over all time shifts.
Differences:
- Representation
of Signals: Discrete-time systems deal with sequences, while
continuous-time systems deal with functions.
- Mathematical
Representation: Discrete-time systems are described using difference
equations, while continuous-time systems are described using differential
equations.
- Impulse
Response: In discrete time, the impulse response is a sequence, while
in continuous time, it is a function.
- Convolution: The convolution operation is performed differently in discrete and continuous time due to the nature of the signals involved.
Q.4 Explain the Fourier transform. Also write any two
properties of Fourier transform.
The Fourier Transform is a powerful mathematical tool used
to decompose a signal into its constituent frequencies. It is widely used in
various fields such as signal processing, communication systems, image
processing, and more.
Fourier Transform:
The Fourier Transform of a signal is a mathematical
operation that transforms a function of time (or space) into a function of
frequency. It allows us to represent a signal in the frequency domain, where we
can analyze its frequency content, amplitude, and phase characteristics.
For a continuous-time signal x(t), the
Fourier Transform X(f) is defined as:
Where:
- x(t)
is the input signal,
- X(f)
is its Fourier Transform, and
- f
represents frequency.
For a discrete-time signal x[n], the
Discrete Fourier Transform (DFT) is used, which is a sampled version of the
continuous Fourier Transform.
These properties make the Fourier Transform an invaluable tool for analyzing and manipulating signals in both time and frequency domains. It allows us to understand the frequency content of signals, filter out unwanted frequencies, and perform operations such as convolution and modulation.
Q.5 Define and explain casual and non-casual system.
Certainly! In the context of signal processing and systems
theory, the terms "causal" and "non-causal" describe
important characteristics of systems based on their response to input signals.
Causal System:
A causal system is one where the output of the system
depends only on present and past values of the input signal, not future values.
In other words, the system's response at any given time is determined solely by
the input values up to that time.
Mathematically, for a continuous-time system, a system H(t)
is causal if:
h(t)=0 for t<0
For a discrete-time system, a system H[n]
is causal if:
h[n]=0 for n<0
In simpler terms, a causal system cannot
"anticipate" or "predict" future input values when
generating its output.
Non-Causal System:
Conversely, a non-causal system is one where the output at a
given time depends on future as well as present and past values of the input
signal. These systems exhibit behavior that violates the principle of
causality.
Mathematically, for a continuous-time system, a system H(t)
is non-causal if it has non-zero response for t<0.
For a discrete-time system, a system H[n]
is non-causal if it has non-zero response for n<0.
Non-causal systems are often theoretical constructs and are
not typically encountered in practical applications because they imply the
ability to predict the future based on present and past observations.
Examples:
- Causal
System: A simple low-pass filter where the output at any time depends
only on the input signal values up to that time.
- Non-Causal
System: A filter that tries to predict future values of a signal based
on present and past values. Such a system would be non-causal, and in
practical terms, it would be difficult to implement because it would
require knowledge of future input values.
Q.6 state and prove sampling theorem
Statement of the Sampling Theorem:
The Sampling Theorem states that:
"A continuous-time signal x(t) can
be perfectly reconstructed from its samples if and only if the sampling
frequency fs is greater than twice the maximum frequency
component fmax present in the signal, i.e. fs>2fmax."
Proof Sketch:
To prove the Sampling Theorem, let's consider a
continuous-time signal x(t) with a bandwidth limited to fmax
Hz.
- Sampling
Process:
- We
sample the continuous-time signal x(t) at a rate of fs
samples per second to obtain the discrete-time signal x[n].
- The
sampling rate fs is measured in samples per
second or Hz.
- Reconstruction:
- According
to the Nyquist-Shannon theorem, x(t) can be
perfectly reconstructed from its samples if the sampling frequency fs
satisfies fs >2fmax.
- Frequency
Domain Analysis:
- In
the frequency domain, the spectrum of x(t) is
limited to fmax Hz.
- Due
to the Nyquist criterion, the spectrum of the sampled signal x[n]
repeats at intervals of fs Hz.
- Avoiding
Aliasing:
- Aliasing
occurs when frequencies above fmax fold back
into the frequency range of interest during sampling, causing distortion.
- To
avoid aliasing, fs must be greater than twice fmax,
ensuring that the spectra of adjacent replicas do not overlap.
- Perfect
Reconstruction:
- With
fs>2fmax, the original
signal x(t) can be perfectly reconstructed from its
samples x[n] using interpolation techniques.
Q.7 Define ROC. State and explain properties of ROC.
Definition of ROC:
The Region of Convergence (ROC) is the set of values of the
complex variable z for which the Z-transform of a discrete-time
signal or system converges. In other words, it is the region in the complex
plane where the Z-transform exists and is finite.
Properties of ROC:
- ROC
Must Include the Unit Circle (Discrete-Time Systems):
- For
a causal and stable discrete-time system, the ROC must include the unit
circle in the z-plane. This ensures convergence and
stability of the system.
- If
the system is anti-causal, the ROC lies outside the unit circle.
- ROC
Is Uniquely Determined:
- The
ROC is uniquely determined by the properties of the discrete-time signal
or system, including its causality, stability, and the nature of the
Z-transform.
- ROC
Is Either Inside or Outside of Singularities:
- The
ROC cannot include any poles of the Z-transform. It must be either inside
or outside of the poles in the z-plane.
- If
the ROC includes the outermost pole, it extends to infinity in that
direction.
- ROC
Can Be Bounded or Unbounded:
- The
ROC can be bounded (limited in extent) or unbounded (extending to
infinity in one or more directions) depending on the properties of the
signal or system.
- ROC
and Causality:
- For
a causal system, the ROC is the region exterior to the outermost pole.
- For
an anti-causal system, the ROC is the region interior to the innermost
pole.
- For
a two-sided system, the ROC is an annular region between the innermost
and outermost poles.
- ROC
and System Stability:
- The ROC provides insights into the stability of the discrete-time system. Generally, a stable system has an ROC including the unit circle.
Q.8 Difference between power signal and energy signal.
Power Signal:
A power signal is a signal for which the total power is
finite and nonzero. It is usually associated with continuous signals that are
non-periodic or with discrete signals that have infinite duration. The power
signal's power is spread out over time.
- Mathematical
Definition: For a continuous-time signal x(t), it
is a power signal if the integral of the squared magnitude of the signal
over time is finite:
- Example:
A sinusoidal signal with finite amplitude and frequency is a power signal.
Energy Signal:
An energy signal is a signal for which the total energy is
finite and nonzero. It is typically associated with signals that are either
finite in duration or have a bounded amplitude.
- Mathematical
Definition: For a continuous-time signal x(t), it
is an energy signal if the integral of the squared magnitude of the signal
over time is finite:
- Example:
A finite-duration rectangular pulse signal with finite amplitude is an
energy signal.
Differences:
- Duration:
- Power
signals may have infinite duration, while energy signals have finite
duration.
- Power
vs. Energy:
- Power
signals have finite power but potentially infinite energy.
- Energy
signals have finite energy but potentially infinite power.
- Application:
- Power
signals are common in continuous communication channels where signals may
be transmitted continuously.
- Energy
signals are common in digital communication systems where signals are
discrete and often have finite duration.
- Analysis:
- Power
signals are analyzed in terms of power spectral density and average
power.
- Energy
signals are analyzed in terms of energy spectral density and total
energy.
|
Aspect |
Power Signal |
Energy Signal |
|
Total Power |
Finite and nonzero |
Infinite or finite |
|
Total Energy |
Potentially infinite |
Finite and nonzero |
|
Duration |
May be infinite |
Finite |
|
Mathematical Condition |
(\int_{-\infty}^{\infty} |
x(t) |
|
Examples |
Sinusoidal signals, periodic signals |
Rectangular pulses, finite-duration signals |
|
Application |
Continuous communication channels |
Digital communication systems |
|
Analysis |
Power spectral density, average power |
Energy spectral density, total energy |
Q.9 Determine the Z transform of the following signal
x(n)= -nan u (n-1).
Q.10 Find Z transform of the function an indicate the ROC
x(n)=n(n+1) ⋅an ⋅u(n).
Q.11 Write short notes on Application of DTFT and Impulse
response of DT-LTI system and its properties.
Application of DTFT (Discrete-Time Fourier Transform):
The Discrete-Time Fourier Transform (DTFT) is a fundamental
tool in digital signal processing for analyzing the frequency content of
discrete-time signals. Here are some key applications:
- Frequency
Analysis: DTFT helps in decomposing a discrete-time signal into its
frequency components. This analysis is crucial for understanding the
spectral characteristics of the signal.
- Filter
Design: DTFT aids in designing digital filters by providing insights
into the frequency response of the system. Engineers can analyze the
behavior of the filter in the frequency domain and optimize its
performance based on desired specifications.
- Spectrum
Analysis: DTFT is used for spectrum analysis of discrete-time signals.
It helps in identifying dominant frequencies, detecting harmonics, and
analyzing periodic signals.
- Signal
Reconstruction: DTFT allows for signal reconstruction from its
frequency components. By knowing the frequency content, one can
reconstruct the original signal using inverse DTFT.
- Fourier
Transform Properties: Many properties of the continuous Fourier
transform extend to the DTFT. These properties provide powerful tools for
signal manipulation, including shifting, scaling, convolution, and
modulation.
Impulse Response of DT-LTI System and its Properties:
A Discrete-Time Linear Time-Invariant (DT-LTI) system is
characterized by its impulse response, which describes the system's behavior
when subjected to a unit impulse input. Here are some key points about the
impulse response of DT-LTI systems:
- Definition:
The impulse response h(n) of a DT-LTI system
represents the output of the system when the input is a unit impulse δ(n).
- Convolution
Integral: The output of a DT-LTI system in response to any input
signal x(n) can be obtained by convolving x(n)
with the impulse response h(n). This convolution
operation is fundamental in analyzing and understanding the behavior of
DT-LTI systems.
- Properties:
- Linearity:
The impulse response of a DT-LTI system exhibits linearity. If h1(n)
and h2(n) are the impulse responses of two systems,
then a1h1(n)+a2h2(n)
is the impulse response of a linear combination a1h1(n)+a2h2(n).
- Time
Invariance: The impulse response of a DT-LTI system is
time-invariant. This means that if the input signal is delayed or
advanced in time, the output is similarly delayed or advanced.
- Causality:
Many practical systems are causal, meaning their impulse response is zero
for negative time indices.
- Stability:
DT-LTI systems are stable if the impulse response is absolutely summable,
i.e.,
- Frequency
Response: The frequency response of a DT-LTI system, denoted by H(ejω),
is the Discrete-Time Fourier Transform (DTFT) of its impulse response.
It provides insights into the system's behavior in the frequency domain
and is crucial for filter design and analysis.
Q.12 Prove the properties of the time shifting in
Z-transform.
The time-shifting property of the Z-transform states that if we shift a discrete-time signal x(n) by k units in time, the Z-transform of the shifted signal x(n−k) is given by z−kX(z), where X(z) is the Z-transform of the original signal x(n). Let's prove this property formally:
Q.13 Parseval's Theorem.
Parseval's theorem, named after the French mathematician
Marc-Antoine Parseval, is a fundamental result in signal processing and Fourier
analysis. It relates the energy of a signal in the time domain to its energy in
the frequency domain. The theorem holds for both continuous and discrete
signals, and it provides an essential tool for signal analysis and system
characterization.
Continuous-Time Case:
For a continuous-time signal x(t) with
its Fourier transform X(f), Parseval's theorem states:
In words, the total energy of the signal x(t)
over all time is equal to the total energy of its Fourier transform X(f)
over all frequencies.
Discrete-Time Case:
For a discrete-time signal x[n] with
its Discrete Fourier Transform (DFT) X[k], Parseval's
theorem states:
In words, the total energy of the discrete-time signal x[n]
over all samples is equal to the sum of the squares of the magnitudes of its
DFT coefficients X[k], normalized by the number of samples
N.
Application and Importance:
- Energy
Conservation: Parseval's theorem ensures that the total energy of a
signal is conserved when transforming between the time and frequency
domains.
- Signal
Analysis: It provides a way to analyze the frequency content of a
signal by examining its energy distribution in the frequency domain.
- System
Characterization: Parseval's theorem is used to analyze the energy
properties of signals processed by linear time-invariant (LTI) systems.
- Filter
Design: Engineers use Parseval's theorem to design filters and ensure
that the filter preserves the signal's energy content.
Q.14 Duality Theorem / Property of Fourier transform states and proved.
The Duality Theorem, also known as the Duality Property of
the Fourier Transform, is a fundamental result in Fourier analysis that
establishes a relationship between a function and its Fourier transform, as
well as between the inverse Fourier transform of a function and its Fourier
dual.




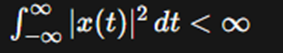





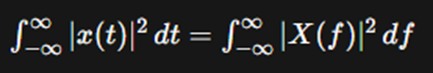
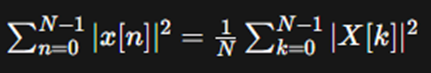












.webp)


0 Comments